Requests 库
robots.txt 网络爬虫排除标准
爬虫协议: http:// robots.txt
实例1.京东商品页面的爬取
实例2.亚马逊商品页面爬取
import requests
url = "https://item.jd.com/100012545852.html"
try:
# 更改头部信息
kv = {'user-agent': 'Mozilla/5.0'}
r = requests.get(url, headers=kv)
r.raise_for_status()
r.encoding = r.apparent_encoding
# print(r.request.headers)
print(r.text[:1000])
except:
print("爬取失败")
实例3.百度,360搜索关键字提交
import requests
url = "https://www.baidu.com/s"
keyword = "Python" #中文也没问题
try:
kv = {'wd': 'keyword'}
r = requests.get(url, params=kv)
# https://www.baidu.com/s?wd=Python
print(r.request.url)
r.raise_for_status() # 1469
r.encoding = r.apparent_encoding
print(len(r.text)) #
print(r.text)
except:
print("爬取失败")
实例4.图片的爬取和抓取
import requests
import os
url = "http://"
root = "D://pics//"
path = root+url.split('/')[-1] #原来的名字储存在本地
try:
if not os.path.exists(root): #根目录是否存在
os.mkdir(root)
if not os.path.exists(path):
r = requests.get(url)
with open(path,'wb') as f:
f.write(r.content)
f.close()
print("文件保存成功")
else:
print("文件已经村在")
except:
print("爬取失败")
实例5. IP地址归属地查询
import requests
#url = "http://m.ip138.com/ip.asp?ip="
url = "https://www.ip138.com/iplookup.asp?ip="
try:
kv = {'user-agent': 'Mozilla/5.0'}
r = requests.get(url + 'IP地址' + '&action=2',headers=kv)
print(r.status_code)
r.encoding = r.apparent_encoding
# 返回最后500字节
#print(r.text[-500:])
print(r.text[:2000])
except:
print("爬取失败")
实例6.多线程对视频爬取
"""使用多线程爬取梨视频视频数据"""
"""https://www.cnblogs.com/zivli/p/11614103.html"""
import requests
import re
from lxml import etree
from multiprocessing.dummy import Pool
url = 'https://www.pearvideo.com/category_5'
page_text = requests.get(url=url).text
tree = etree.HTML(page_text)
# 1、获取页面中视频详情地址
li_list = tree.xpath('//ul[@id="listvideoListUl"]/li')
url_list = []
for i in li_list:
# 2、构造出每个视频的详情地址
detail_url = "https://www.pearvideo.com/" + i.xpath('./div/a/@href')[0]
name = i.xpath('./div/a/div[2]/text()')[0] + '.mp4'
# 3、向视频详情地址发起请求
detail_page = requests.get(url=detail_url).text
# 4、从response中解析出视频的真实地址
ex = 'srcUrl="(.*?)",vdoUrl'
video_url = re.findall(ex, detail_page)[0]
dic = {
'name': name,
'url': video_url
}
url_list.append(dic)
def get_video_data(d):
"""
向视频地址发起请求,二进制写入本地文件
:param d:
:return:
"""
url = d['url']
data = requests.get(url=url).content
print(d['name'], "正在下载。。。")
with open(d['name'], 'wb') as f:
f.write(data)
print(d['name'], "下载成功。。。")
# 使用多进程处理
pool = Pool(4)
pool.map(get_video_data, url_list)
pool.close()
pool.join()BeautifulSoup库


from bs4 import BeautifulSoup
soup = BeautifulSoup('<p>data</p>','html.parser')
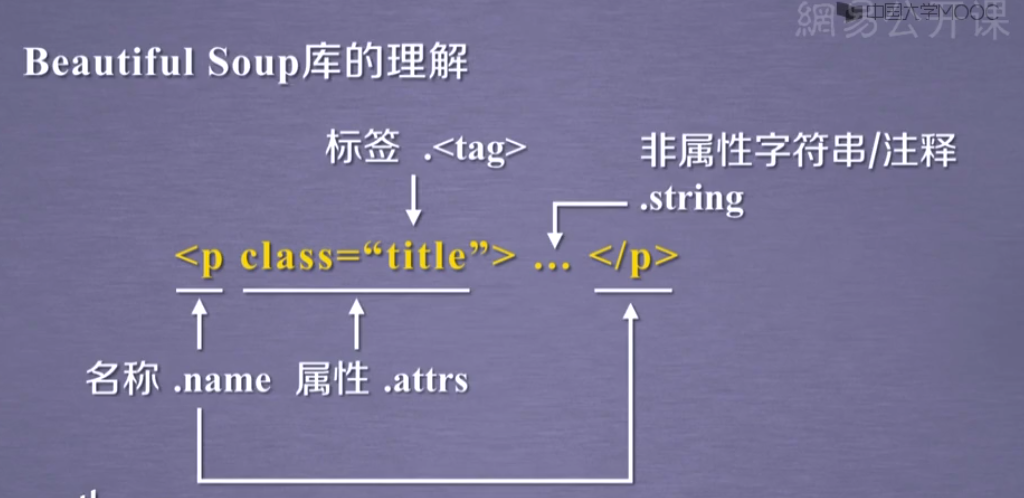
"""Beautiful Soup库的基本元素"""
import requests
from bs4 import BeautifulSoup
url = "https://python123.io/ws/demo.html"
r = requests.get(url)
demo = r.text
soup = BeautifulSoup(demo, "html.parser")
#print(soup.prettify())
# <title>This is a python demo page</title>
print(soup.title)
tag = soup.a
# <a class="py1" href="http://www.icourse163.org/course/BIT-268001" id="link1">Basic Python</a>
print(tag)
# a
print(soup.a.name)
# p
print(soup.a.parent.name)
# body
print(soup.a.parent.parent.name)
# html
print(soup.a.parent.parent.parent.name)
# [document]
print(soup.a.parent.parent.parent.parent.name)
# {'href': 'http://www.icourse163.org/course/BIT-268001', 'class': ['py1'], 'id': 'link1'}
print(tag.attrs)
# ['py1']
print(tag.attrs['class'])
# http://www.icourse163.org/course/BIT-268001
print(tag.attrs['href'])
# <class 'dict'>
print(type(tag.attrs))
# <class 'bs4.element.Tag'>
print(type(tag))
# Basic Python
print(soup.a.string)
# <p class="title"><b>The demo python introduces several python courses.</b></p>
print(soup.p)
# The demo python introduces several python courses.
print(soup.p.string)
# <class 'bs4.element.NavigableString'>
print(type(soup.p.string))
基于bs4库的HTML内容遍历方法
根据树形结构,有三种遍历方式:上行,下行和平行
下行:.contents 列表类型
.children 循环类型
.decendants
上行:.parent
:.parents
for parent in soup.a.parents:
if parent is None:
print(parent)
else:
print(parent.name)
平行:.next_sibling
.previous_sibling
.next_siblings
.previous_siblings
基于bs4库的html格式化
.prettify()
#bs4库使用utf-8编码方式与Python3.X匹配信息的标记
HTML,XML,一对标签
JSON 有类型的键值对构成的表达形式
YAML 无类型键值对 key:value
import requests
from bs4 import BeautifulSoup
url = "https://python123.io/ws/demo.html"
r = requests.get(url)
demo = r.text
soup = BeautifulSoup(demo, "html.parser")
for link in soup.find_all('a'):
print(link.get('href'))
# http://www.icourse163.org/course/BIT-268001
# http://www.icourse163.org/course/BIT-1001870001
基于bs4库的HTML内容查找方法.png)
.png)
.png) 的最大值。
的最大值。.png) ( 其中λk是各个约束条件的待定系数。)
( 其中λk是各个约束条件的待定系数。).png) …
….png)
.png)
.png) 求偏导得到
求偏导得到.png)
.png) 和
和.png) ,带入第四个方程解之
,带入第四个方程解之.png)
.png)
.png)
.png)
.png)
.jpg)
.jpg)